Inductances
From Eric
m |
|||
| Line 1: | Line 1: | ||
| - | = | + | = Mesure d'une inductance = |
| - | + | Le principe consiste à soumettre un circuit RLC, où L est inconnu, à un signal sinusoïdal de caractéristiques connues, et à observer sa réponse. | |
| - | + | Tout d'abord, quelques rappels sur les impédances complexes... | |
| - | == | + | == Les impédances en courant alternatif == |
| - | == | + | === La résistance === |
| - | + | L'impédance d'une résistance est réelle pure, de module ZR = R. Une résistance ne n'introduit ni retard ni avance entre courant et la tension. | |
| - | + | === La capacité === | |
| - | + | L'impédance d'un condensateur se calcule ainsi : | |
| - | |||
| - | + | Si on considère que | |
| + | * U = U0 e^(jwt) | ||
| + | * I = I0 e^(jwt+phi) = I0 ( cos (wt+phi) + j sin (wt +phi) ) | ||
| - | + | Aux bornes du condensateur, on a UC = ZC * I = 1/(jwC) I = -j/(wC) I = 1/(wC) (sin (wt +phi) + j cos (wt + phi)) = U0 (sin (wt) + j cos (wt) ) | |
| + | |||
| + | d'où phi = pi/2 | ||
| + | |||
| + | Aux bornes d'un condensateur, le courant est en avance de pi/2 sur la tension. | ||
| + | |||
| + | === L'inductance === | ||
L'impédance d'une inductance se calcule ainsi : | L'impédance d'une inductance se calcule ainsi : | ||
| + | L'inductance a un effet inverse de celle d'un condensateur sur la relation entre courant et tension : aux bornes d'une inductance, le courant est en retard de pi/2 sur la tension. | ||
Considérons maintenant un circuit RLC série. | Considérons maintenant un circuit RLC série. | ||
| Line 38: | Line 46: | ||
Pour estimer la valeur de L, je soumets donc mon circuit RLC à une fréquence F que je fais varier jusqu'à ce que le circuit soit en résonance. Je mesure la fréquence F, je connais la valeur de C (soit en me fiant à ce qui est écrit sur le composant, soit en mesurant sa valeur, ce que la plupart des multimètres savent faire), donc je trouve L. | Pour estimer la valeur de L, je soumets donc mon circuit RLC à une fréquence F que je fais varier jusqu'à ce que le circuit soit en résonance. Je mesure la fréquence F, je connais la valeur de C (soit en me fiant à ce qui est écrit sur le composant, soit en mesurant sa valeur, ce que la plupart des multimètres savent faire), donc je trouve L. | ||
| - | + | == Mise en oeuvre == | |
| - | + | ||
Considérons le circuit RLC ci-après, où R=1K, C=467uF et L est inconnu (on ne triche pas...) : | Considérons le circuit RLC ci-après, où R=1K, C=467uF et L est inconnu (on ne triche pas...) : | ||
| Line 68: | Line 75: | ||
valeur qui est (ma foi) assez proche de celle indiquée sur le composant, à savoir : 180uH. | valeur qui est (ma foi) assez proche de celle indiquée sur le composant, à savoir : 180uH. | ||
| + | |||
| + | = Marquage des inductances = | ||
| + | <A compléter> | ||
| + | |||
| + | = Calcul d'une inductance = | ||
| + | |||
| + | == Bobine à une couche, air == | ||
| + | <A compléter> | ||
| + | |||
| + | == Bobine longue à plusieurs couches, air == | ||
| + | <A compléter> | ||
| + | |||
| + | == Bobine courte à plusieurs couches, air == | ||
| + | <A compléter> | ||
Revision as of 13:06, 8 May 2011
Contents[hide] |
Mesure d'une inductance
Le principe consiste à soumettre un circuit RLC, où L est inconnu, à un signal sinusoïdal de caractéristiques connues, et à observer sa réponse.
Tout d'abord, quelques rappels sur les impédances complexes...
Les impédances en courant alternatif
La résistance
L'impédance d'une résistance est réelle pure, de module ZR = R. Une résistance ne n'introduit ni retard ni avance entre courant et la tension.
La capacité
L'impédance d'un condensateur se calcule ainsi :
Si on considère que
- U = U0 e^(jwt)
- I = I0 e^(jwt+phi) = I0 ( cos (wt+phi) + j sin (wt +phi) )
Aux bornes du condensateur, on a UC = ZC * I = 1/(jwC) I = -j/(wC) I = 1/(wC) (sin (wt +phi) + j cos (wt + phi)) = U0 (sin (wt) + j cos (wt) )
d'où phi = pi/2
Aux bornes d'un condensateur, le courant est en avance de pi/2 sur la tension.
L'inductance
L'impédance d'une inductance se calcule ainsi :
L'inductance a un effet inverse de celle d'un condensateur sur la relation entre courant et tension : aux bornes d'une inductance, le courant est en retard de pi/2 sur la tension.
Considérons maintenant un circuit RLC série.
L'impédance du circuit est la somme des impédances, soit Z = R+jLw+1/(jCw) = R+j(Lw-1/(Cw))
U = Z I donc si Z est réelle, alors le déphasage entre I et U est nul et, par conséquent, le déphasage entre la tension mesurée aux bornes de la résistance et la tension aux bornes du circuit RLC est nul lui aussi, et réciproquement. Dans cette situation, le circuit est en résonance avec le signal d'entrée (le signal d'excitation).
Z est réelle si Lw-1/(Cw) = 0 <=> w^2 = 1/(LC) <=> w = sqrt(1/(LC))
Or w = 2*Pi*F
Donc (2*Pi*F)^2 = 1/(LC) <=> L = 1/((2*Pi*F)^2*C)
Pour estimer la valeur de L, je soumets donc mon circuit RLC à une fréquence F que je fais varier jusqu'à ce que le circuit soit en résonance. Je mesure la fréquence F, je connais la valeur de C (soit en me fiant à ce qui est écrit sur le composant, soit en mesurant sa valeur, ce que la plupart des multimètres savent faire), donc je trouve L.
Mise en oeuvre
Considérons le circuit RLC ci-après, où R=1K, C=467uF et L est inconnu (on ne triche pas...) :
Je soumets le circuit à une fréquence F :
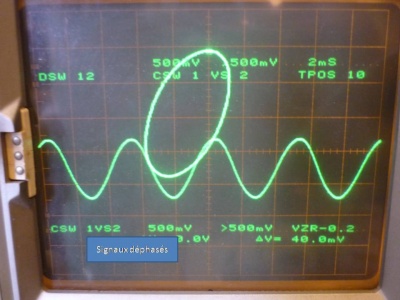
On constate manifestement que le déphasage est non nul. En configurant l'oscilloscope pour que le balayage en X soit piloté par une voie et que le balayage en Y soit piloté par la seconde voie, on constate très clairement que les deux signaux ne sont pas en phase : s'ils l'étaient, on observerait une droite (d'équation Y=X).
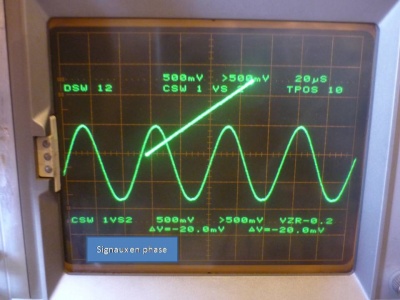
En changeant la valeur de la fréquence, on parvient à atteindre la résonance :
Ce qui est encore plus clair en observant la courbe de Lissajou :
On peut alors estimer L :
- Les indications de l'oscilloscope nous donnent P = 50us => F = 20000Hz
- On sait que C = 467nF
d'où L = 1/((2*Pi*F)^2*C) = 1/ ((2*3.14*20000)^2*467.10^-9) = 1.35*10-4 H = 135.10^-6 = 135 uH
valeur qui est (ma foi) assez proche de celle indiquée sur le composant, à savoir : 180uH.
Marquage des inductances
<A compléter>
Calcul d'une inductance
Bobine à une couche, air
<A compléter>
Bobine longue à plusieurs couches, air
<A compléter>
Bobine courte à plusieurs couches, air
<A compléter>